
昨天認識了什麼是 Applicative,今天會再介紹 Applicative 要遵守的定律,以及更多應用範例~
就像 Functor 和 Monad 一樣,Applicative 也要遵守一些定律。這些定律保證 Applicative 的行為是可預測且可靠的,讓我們可以安心地進行抽象和重構。
A.of(id).ap(v)必須等價於v
以程式來看就是A.of(id).ap(v) === v;
將一個包裹著恆等函數 (x => x) 的值應用到一個包裹著的值 v 上,結果應該等於原來的 v。這就像在一般值的世界裡,id(x) 等於 x 一樣。此定律保證 of 所建立的 context(容器) 是「中性」的,它在透過 ap 組合時不會改變另一個值的 context。
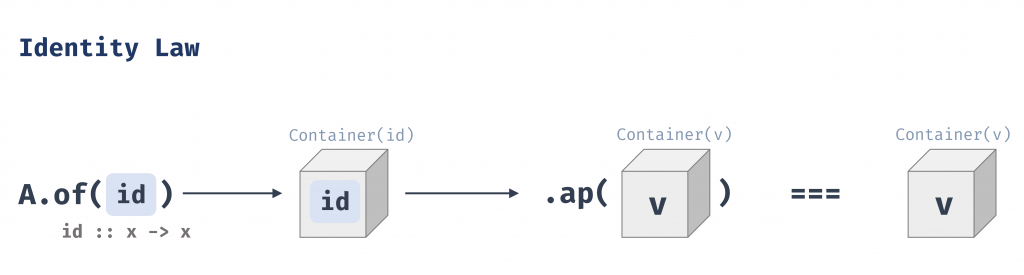
圖 1 同一律示意圖(資料來源: 自行繪製)
舉例來說,Maybe.of(x => x).ap(Maybe.of(10)) 的結果必須是 Maybe.of(10)。
由此可知,of 搭配 ap 與 map 是等價的,因為此 Identity Law 就是直接來自於 Functor 的 Identity Law:map(id) == id
A.of(f).ap(A.of(x))必須等價於A.of(f(x))
以程式來看就是A.of(f).ap(A.of(x)) === A.of(f(x));
同態的意思是「結構保持的映射」(A homomorphism is just a structure preserving map.),具體的意思是,將一個包裹起來的函數 f 應用到一個包裹起來的值 x 上,其結果應該與先將一般函數 f 應用到一般值 x 上,再將結果包裹起來,是完全一樣的。
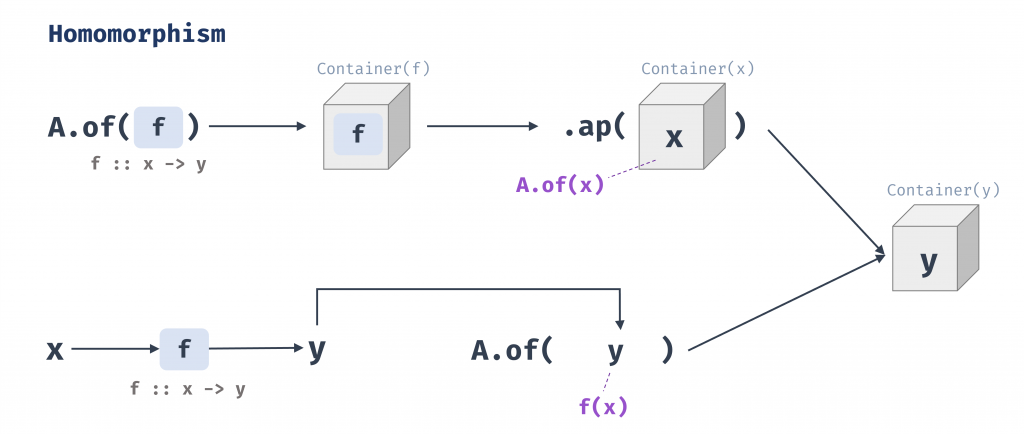
圖 2 同態律示意圖(資料來源: 自行繪製)
這條定律是「兩個世界」比喻的數學保證:它證明了 of 純粹是兩個世界之間的「傳送門」,將計算從一般值的世界提升到容器世界,而不會扭曲計算本身的結果。
舉例來說:
Maybe.of(x => x * 2).ap(Maybe.of(5)) === Maybe.of((x => x * 2)(5))
// 結果都是 Maybe.of(10)
而其實 Functor 的 map 也符合這個定律,它在 map 的過程中保持了原始資料的結構,例如 Maybe.of(2).map(x => x + 1) 會得到 Maybe.of(3),map 過程中都還是保有原本的 Maybe 結構
g.ap(A.of(x))必須等價於A.of(f => f(x)).ap(g)
以程式來看就是g.ap(A.of(x)) === A.of(f => f(x)).ap(g);
這條定律的核心思想是「獨立性」。
g 是一個包裹起來的函數,將這個包裹起來的函數 g 應用到一個包裹起來的值 x 上(左側),等同於先建立一個「應用器」函數 f => f(x)(一個會將任何傳入的函數應用到 x 值上的函數),將這個應用器函數包裹起來,再把它應用到我們最初的包裹函數 g 上(右側)。
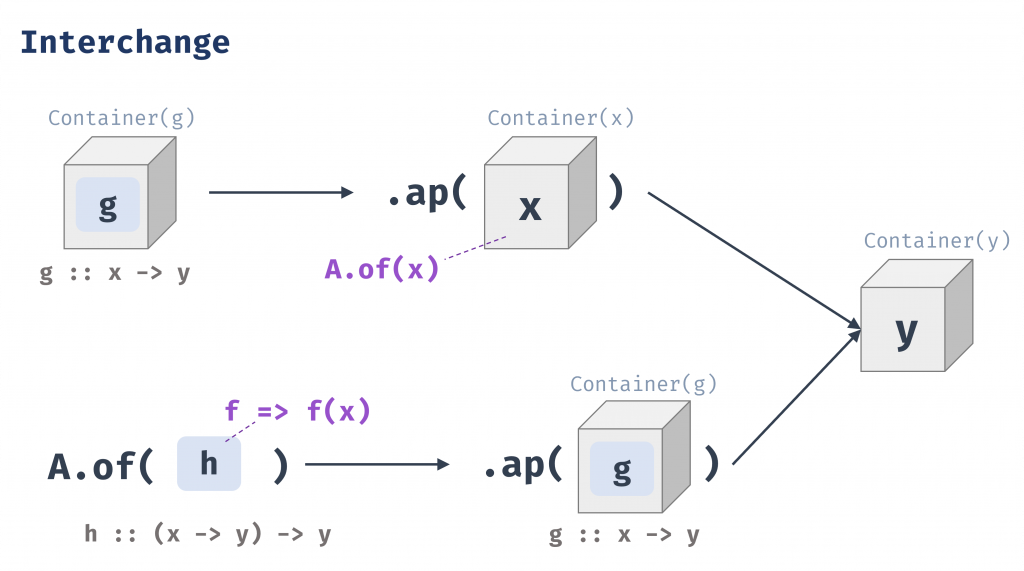
圖 3 交換律示意圖(資料來源: 自行繪製)
簡言之,包裹的函數和包裹的值在被 ap 結合之前是互相獨立的,它們的求值順序並不重要。
舉例來說:
const v = Task.of(reverse);
const x = 'opanchu';
v.ap(Task.of(x)) === Task.of(f => f(x)).ap(v);
A.of(compose).ap(u).ap(v).ap(w)必須等價於u.ap(v.ap(w))
以程式來看就是A.of(compose).ap(u).ap(v).ap(w) === u.ap(v.ap(w));
這條定律確保 Applicative 運算的組合是符合結合律的,就像一般函數的組合一樣。這讓我們能安心地將一連串的 ap 操作鏈接在一起,而不用擔心它們的組合順序會影響最終結果。
這定律也展現出 Applicative 與 Monoid 之間的關聯。Monoid 的核心特性就是一個符合結合律的二元操作,而組合律確保 Applicative 的 ap 操作也具備這種性質。當我們用 Applicative 來累積錯誤時,可依賴這定律來保證 (e1 + e2) + e3 和 e1 + (e2 + e3) 的結果是一樣的。
以下再舉更多 Applicative 應用案例,以理解實務上會如何使用 Applicative。
當使用者提交一個註冊表單時,通常希望一次告訴他所有欄位的錯誤,而不是讓他改完一個錯的欄位後,提交後他又看到下一個錯誤。
Either 結構天生就是「短路」的。一旦遇到第一個 Left (錯誤),整個計算鏈就會停止,並直接回傳那個 Left,也就是說如果第一個表單欄位錯誤,就會直接回傳錯誤,不管後續欄位的錯誤狀況,但這不是我們期望的,我們希望取得所有表單欄位的驗證結果。
為了解決這個問題,我們可以設計一個 Validation 型別。它的結構和 Either 完全一樣(一個成功態 Success,一個失敗態 Failure),但它的 Applicative 實作卻截然不同:它會累積錯誤 。
// Validation 型別
class Success {
constructor(value) { this.$value = value; }
map(fn) { return new Success(fn(this.$value)); }
ap(otherValidation) {
return otherValidation.isSuccess
? otherValidation.map(this.$value)
: otherValidation;
}
}
Success.prototype.isSuccess = true;
class Failure {
constructor(value) { this.$value = value; }
map(fn) { return this; }
ap(otherValidation) {
// 關鍵:如果另一個也是 Failure,就合併錯誤!
return otherValidation.isSuccess
? this
: new Failure(this.$value.concat(otherValidation.$value));
}
}
Failure.prototype.isSuccess = false;
const Validation = {
of: (value) => new Success(value)
};
在 Failure.ap 的實作中,當它應用於另一個 Failure 時,它不會像 Either 一樣直接回傳自己,而是用 .concat() 將兩個錯誤陣列合併起來。
要讓錯誤能夠被「累積」,錯誤的型別本身必須是一個 Semigroup——也就是一個定義了如何將兩個同類型的值合併成一個新值的型別。陣列的 concat 就是一個標準的 Semigroup 操作。這也顯示 Applicative 的本質:它是一個 Monoidal Functor,它利用 Monoid/Semigroup 的結構來組合容器內的結果。
現在我們來看如何用 Validation 來驗證:
// 驗證規則
const validateUsername = (username) =>
username.length >= 4
? new Success(username)
: new Failure(['Username must be at least 4 characters long.']);
const validateEmail = (email) =>
/^\w+((-\w+)|(\.\w+))*\@[A-Za-z0-9]+((\.|-)[A-Za-z0-9]+)*\.[A-Za-z]+$/.test(email)
? new Success(email)
: new Failure(['Email must be valid.']);
const validatePassword = (password) => {
const errors = [];
if (!password || password.length < 8) errors.push('Password must be at least 8 characters.');
if (!/[A-Z]/.test(password)) errors.push('Password must contain an uppercase letter.');
if (!/[0-9]/.test(password)) errors.push('Password must contain a digit.');
return errors.length ? new Failure(errors) : new Success(password);
};
// 柯里化的成功回呼
const registrationSuccess =
curry((username, email, password) => ({
username, email, password, status: 'validated'
}));
// --- 進行驗證(Applicative 風格) ---
const validateRegistration = (username, email, password) =>
Validation.of(registrationSuccess)
.ap(validateUsername(username))
.ap(validateEmail(email))
.ap(validatePassword(password));
// --- 測試 ---
console.log(
validateRegistration('mo', 'invalid-email', 'abc')
);
// Failure([
// "Username must be at least 4 characters long.",
// "Email must be valid.",
// "Password must be at least 8 characters.",
// "Password must contain an uppercase letter.",
// "Password must contain a digit."
// ])
console.log(validateRegistration('monicaaa', 'hello', 'password12'))
// Failure([
// "Email must be valid.",
// "Password must contain an uppercase letter."
// ])
console.log(
validateRegistration('monica', 'monica@example.com', 'StrongP4ss')
);
// Success({ username: 'monica', email: 'monica@example.com', password: 'StrongP4ss', status: 'validated' })
當多個欄位都驗證失敗時,Validation Applicative 成功地將所有錯誤訊息搜集到一個陣列中,符合我們預期的使用者體驗。(完整程式可見此連結。)
另外我們還可進一步將連續的 .ap 改用 liftA3 來讓程式更簡潔。
const liftA3 = curry((fn, applicative1, applicative2, applicative3) =>
applicative1.map(fn).ap(applicative2).ap(applicative3)
);
// --- 用 liftA3 改寫驗證流程 ---
const validateRegistration = (username, email, password) =>
liftA3(
registrationSuccess,
validateUsername(username),
validateEmail(email),
validatePassword(password)
);
// --- 測試 ---
console.log(
validateRegistration('mo', 'invalid-email', 'abc')
);
// Failure([
// "Username must be at least 4 characters long.",
// "Email must be valid.",
// "Password must be at least 8 characters.",
// "Password must contain an uppercase letter.",
// "Password must contain a digit."
// ])
console.log(validateRegistration('monicaaa', 'hello', 'password12'))
// Failure([
// "Email must be valid.",
// "Password must contain an uppercase letter."
// ])
console.log(
validateRegistration('monica', 'monica@example.com', 'StrongP4ss')
);
// Success({ username: 'monica', email: 'monica@example.com', password: 'StrongP4ss', status: 'validated' })
一樣只要 Failure.ap(Failure),就透過 concat 把錯誤累積起來;任一位置成功/失敗都能正確折疊出總體結果。
Monad 的 chain 本質上是循序的,一個計算必須等待前一個計算完成才能開始。但某些情況下計算是互相獨立的,不需要等待,此時可用 Applicative。
假設有個應用要同時取得觀光景點與當地活動的 API 資料,我們可用 ap 來讓兩個 API 呼叫同時執行,不會互相等待,且 renderPage 會在兩個 Task 都 resolve 之後才執行。
const delay = (ms: number): Promise<void> => new Promise(resolve => setTimeout(resolve, ms))
const Http = {
get: (url: string): T.Task<string> => async () => {
const simulatedLatencyMs = url.includes('destinations') ? 600 : 300
await delay(simulatedLatencyMs) // 簡單模擬網路請求
return `data-from-${url}`
},
}
const renderPage = (destinationsHtml: string) => (eventsHtml: string): string =>
`<div>page: destinations=${destinationsHtml}; events=${eventsHtml}</div>`
// 平行發出 Task 中的 http 請求
const programPar: T.Task<string> = pipe(
T.of(renderPage),
T.ap(Http.get('/destinations')),
T.ap(Http.get('/events')),
)
另外寫個序列執行的方法,等等可以比較執行時間:
// 透過 chain 序列式執行 Task
const programSeq: T.Task<string> = pipe(
Http.get('/destinations'),
T.chain(destinationsHtml =>
pipe(
Http.get('/events'),
T.map(eventsHtml => renderPage(destinationsHtml)(eventsHtml)),
),
),
)
最後看看兩種方式實際執行所花的時間:
const run = async (): Promise<void> => {
console.time('ap')
const htmlPar = await programPar()
console.log('[ap]', htmlPar)
console.timeEnd('ap')
console.time('monad')
const htmlSeq = await programSeq()
console.log('[monad]', htmlSeq)
console.timeEnd('monad')
}
run()
可看出 monad 序列寫法的執行時間是 300 + 600 大概 900 ms 左右,而 Applicative 並行的寫法執行時間是 Math.max(300, 600),兩者取最大值大約 600 ms 左右,由此看出當兩個請求不相依時,可用 Applicative 的方式並行發出請求來讓程式執行更有效率。
完整程式可見此連結。
目前我們看到的 Applicative 容器 (Maybe、Either、Task) 通常都只包含一個值(或沒有值)。但如果容器本身就可以包含多個值,例如陣列,那 ap 的行為會是什麼樣子呢?
當我們將一個包含多個函數的陣列 ap 到一個包含多個值的陣列上時,會發生一種有趣的現象:
// 假設我們在 JavaScript Array.prototype 上實現 ap
Array.prototype.ap = function (arr) {
return this.flatMap(fn => arr.map(fn));
};
const funcs = [x => x * 2, x => x + 10];
const values = [1, 3, 5];
funcs.ap(values);
// => [2, 6, 10, 11, 13, 15]
說明一下運作流程:
x => x * 2,map 到 values:values.map(x => x * 2) // [2, 6, 10]
x => x + 10,map 到 values:values.map(x => x + 10) // [11, 13, 15]
flatMap 把兩個結果接起來(concat/扁平化):[2, 6, 10, 11, 13, 15]
這種神奇的整合結果可以被理解為一種「非確定性」的計算或結果的「笛卡兒積」(Cartesian Product)。可以把陣列看作是某個計算所有可能結果的集合。
['a', 'b'] 表示結果可能是 'a' 或 'b',因此 [f, g].ap([x, y]) 的意義就是:計算所有可能的函數應用組合。也就是 [f(x), f(y), g(x), g(y)]。
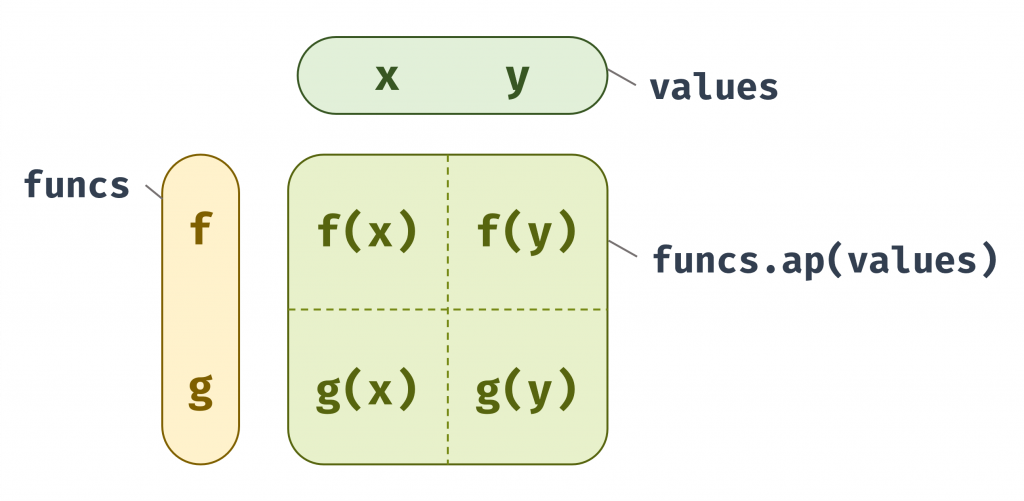
圖 4 陣列中是某計算所有可能結果的集合(資料來源: 自行繪製)
再看一個字串例子:
const join = a => b => a + b;
const prefixes = [join('pre-'), join('super-')];
const bases = ['fix', 'set'];
prefixes.ap(bases);
// => ['pre-fix', 'pre-set', 'super-fix', 'super-set']
// f(x) f(y) g(x) g(y)
最後輸出的陣列會是「函數陣列的順序 × 值陣列的順序」,另外如果陣列中有重複值或函數,會照樣產生對應次數的結果(因為就是列舉所有組合)。
另外還有一個等價寫法是:
const ap = (fs, xs) => fs.flatMap(f => xs.map(f));
ap(funcs, values); // [2, 6, 10, 11, 13, 15]
ap(funcs, values) 這種特性適合處理組合、排列或需要探索所有可能性的情境,這種多可能性的狀況可能會讓人聯想到解析器或規則引擎的應用,不過在解析器或規則引擎中,雖然我們也會遇到「一個輸入對應多個可能結果」的情況,但它們的內部實作並不是直接用 Applicative 的 ap(funcs, values)。
雖然實作方式不同,但這些概略上都可以用「非確定性、多分支」這個概念來理解。
補充:解析器和規則引擎
- 解析器 (Parser):字串轉成結構化資料的工具,常見於編譯器、設定檔讀取,甚至日期格式解析。解析時可能有多種可能性,同一輸入可能有多種切法,例如
12a可解讀為「12+a」或「1+2a」,解析器就會回傳多個結果。- 規則引擎 (Rules Engine):根據一組定義好的條件規則,決定要執行哪些動作的系統。例如,行銷自動化可能設定「如果使用者滿足 A 條件就寄優惠券,如果滿足 B 條件就加到名單」。JavaScript 裡常見的 json-rules-engine 就能做到這件事,它會檢查一個輸入資料物件,觸發所有符合的規則,最後回傳被觸發的規則清單。
用幾個簡單的問題來總結昨天和今天學到的內容。
因為 Functor 的 map 無法處理「函數也被包裹在容器裡」的情況,而 Monad 的 chain 雖然可以透過組合解決問題,但會強加不必要的「循序執行」,對於可以並行處理的獨立任務來說效率較低。Applicative 解決了這兩個問題,可用來組合多個獨立的、帶有 context 的計算。
chain 來巢狀地、循序地處理它們。在表單驗證中,我們只能得到第一個錯誤,無法收集所有錯誤。ap 或 liftA2 等工具,以一種宣告式、類似普通函數呼叫的風格來組合這些值。這讓程式碼不僅更清晰,還能讓底層實作去進行並行化。在驗證場景中能更易實現錯誤累積。可將 Applicative 想成一種更嚴格的 Functor,它定義在一個容器型別上,提供了兩個核心操作:
ap:將一個在容器裡的函數,應用到另一個在同類型容器裡的值of:將一個一般值放入容器的預設 context 中